继续上一次的 拯救007 再上一个问题的基础上 告诉他 能跳上岸的最短步骤.
最短路径 最短的路 最便宜的路 都是最短路径
最短路径的衡量是 其权重大小 权重可以是 时间 路程 花费 站点数
最短路径问题的抽象
在网络中,求两个不同定点之间的所有路径中,边的权值之和最小的那一条路径.
这条路径就是两点之间的最短路径(Shortest)
第一个定点为源点(Source)
最后一个顶点为终点(Destination)
问题分类
单源最短路径问题:从某固定源点出发,求其到所有其他顶点的最短路径.
(有向)无权图
按照递增(非递减)的顺序找出到各个项点的最短路
有向无权图 的 单源路径最短问题的分析步骤就在上面的图里.
void FBS(Vertex S) //传送过来 一个图{ visited[S]=ture; //访问第一个节点 Enqueue(S,Q); //将第一个 节点入队 while(!IsEmpty[Q]) //队列不为空的话 继续进行 { v=Dequeue(Q); //让 节点出队 并且赋值 给v for(V的每个临接点W) //用v的每个临接点轮番轰炸 { if(!visited[W]) // 没有访问的话 { visited[W]=ture; //访问一下 Enqueue(W,Q); //并且 入队 } } }}//dist[w] = s到w的最短距离. //dist 可以起到 visited的作用//dist[s] = 0//path[w] = s到w的路上经过的某顶点 /*上面的 只是一个 广度优先搜索的 框架 在下面 加以改进 用于拯救007*/void Unweighted(Vertex S){ Enqueue(S,Q); //对 第一个节点 入队 while(!IsEmpty(Q)) //队列 不为空 { V=Dequeue(Q); //队列里最前面的 节点出队 for(V的每个临接点 W) // { if(dist[w]==-1) // 默认的是 距离为 -1 如果是-1的话 就代表 没有 到过这个节点 { dist[w]=dist[v]+1; //这个节点等于上一个节点的距离+1 path[w]=v; //这个节点的上一个节点是v w节点的上一个节点是v Enqueue(W,Q); // 仔细观察 这里 和 for循环 那里. } } }}
(有向)有权图
多源最短路径问题:求任意两点之间的最短路径.
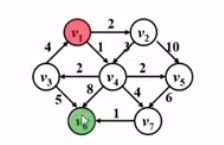从 v1到v6的最短路径是什么?
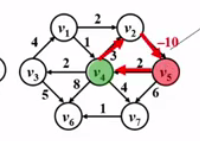这个呢? (以后不做考虑). ---负无穷
Dijkstra算法
令S={源点S+已经确定了最短路径的顶点v1}
对于任意一个未收录的顶点v,定义dist[v]为s到v的最短路径长度,但该路径仅经过S中的顶点.即路径{s->(vi∈s)->v}的最小长度
若路径是按照递增(非递减)的顺序生成的则
真正的最短路必须只经过S中的顶点.
每次从未收录的顶点中选取一个dist最小的收录(贪心)
/*可能有思想原因,身体原因,或者这个算法 难理解 我是用了一天 现在 应该差不多知道了一点*/void Dijkstra(Vertex s){ while(1) { V=未收录的顶点中dist最小者 //和源点相邻的 是权 不相邻的是 正无穷 if(这样的V不存在) break; collected[V]=ture; for(V的每个临接点W) { if(collect[W]==false&&dist[V]+E < dist[W]) { dist[W]=dist[V]+E ; path[W]=V; } } }}//根据图 自己做了一半模拟之后 顿感666
下面附上 上面伪代码里面 " V=未收录的顶点中dist最小者 "的实现方法.
//这里给出两种 实现上述功能的算法,但是相比之下 还是使用传统的算法 好一点简单省力 程序短. 方法1 ：直接扫描所有未收录顶点 – O( |V| ) T = O( |V| 2 + |E| ) 方法2 ：将dist 存在最小堆中 – O( log|V| ) 更新dist[w]值 的值 – O( log|V| ) T = O( |V| log|V| + |E| log|V| ) = O( |E| log|V| )
-------------被 单源最短路径坑了半天---下面开始多元路径问题了----------------------
//多元最短路算法 --可以用单源最短路径算法 每个节点 都调用一次//这样的话时间复杂度是 V^3 + E *V //所谓的Floyd算法 时间复杂度是 V^3 鉴于这种 操蛋的情况 还是了解一下算了//到时候不会用.